洛伦兹因子和洛伦兹变换的起源及其物理学意义的分析
Original Lorentz Factor and Lorentz Transformation
Xia, Cheng; xc7788@gmail.com ; 2010.04.18.
摘要:通过考证洛伦兹因子(Lorentz factor)的起源和其形成过程,揭示了洛伦兹因子和洛伦兹变换(Lorentz transformation)与狭义相对论(Special Relativity)变换方程在物理理论上有本质的区别,首次提出以命名“爱因斯坦变换”或“狭义相对论变换”或“时空变换”的方式来区别这种物理理论的不同内涵。
关键词:洛伦兹因子(Lorentz factor),洛伦兹变换(Lorentz transformation),狭义相对论(Special relativity),“以太”(ether),爱因斯坦变换(Einstein transformation), 狭义相对论变换(Special Relativity transformation), 时空变换(Spacetime transformation)
引言:洛伦兹因子(Lorentz factor)究竟是如何来的?又有什么样的物理意义?洛伦兹的洛伦兹变换(Lorentz transformation)和狭义相对论的变换方程是一样的物理内涵吗?这些都是狭义相对论的重要理论问题,有必要在理论上对此作出答复。
当今,普遍把洛伦兹变换当成为狭义相对论的一部分,洛伦兹因子成为一个出现在狭义相对论中的速记因子,它代表了相对论的效应,其定义式如下:
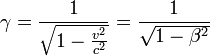
其中β代表了v/c,即物体速度与光速的比值。
那么,如果考证洛伦兹因子的起源和其物理上的涵义,检验洛伦兹的的洛伦兹变换和爱因斯坦的狭义相对论的变换方程,可以发现它们之间有本质的物理理论上的区别。
一 洛伦兹因子的起源
荷兰物理学家洛伦兹(劳仑兹)(Hendrik Lorenz)一生实际是以“以太”[*]理论(Lorentz Ether theory) 而闻名于世,他根据自己的理论,理论性地解释了塞曼效应(Zeeman effect),因此而获得1902年物理学诺贝尔奖。
在1892-1895年期间,洛伦兹最初的理论是基于“以太”(ether)静止[1],但他的这个理论解释不了“以太漂移实验”(aether drift experiments),因此,洛伦兹引入了以“v/c”作为“当地时间”(local time)的概念来将运动的“以太”和静止的“以太”联系起来,其公式是“t‘ = t − vx / c2 ”,其中,“t”表示观察者静止于“以太”中的时间,而“t’”表示观察者和“以太”一起运动时的时间。其数学方法就是洛伦兹因子的起源[2]。
在伽利略变换的基础上,洛伦兹引入了一种“以太”系与运动系进行变换的定量方程式,这也就是洛伦兹变换的起源,即:
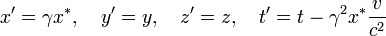
其中,x *是伽利略变换的“x-vt”; t是在“以太”中观察者的“真正”时间,t’为辅助变量只用于运动系的计算过程。
二 洛伦兹因子的形成过程
1879年,麦克斯韦在一封信中指出:“地面上测量光速的方法,光延同样的路径返回,所以地球相对于以太的速度对双程时间的影响取决于地球速度与光速之比的平方(v2/c2),这个量太小了,难以观测。”
1887年,迈克尔逊设计出了一种方案,利用相互垂直的两束光产生干涉的方法来比较光速的差异。假设”以太风”是在横向的,则横向光束传播一个来回需要用时和在纵向光束传播一个来回需要用时有差别。由此可计算出光产生干涉条纹移动的预期值。但他所观察到的条纹移动远远小于预期值。这个实验结果是对静止“以太”理论的一个挑战。
1889年,奥利弗希维赛德(Oliver Heaviside)从麦克斯韦方程组(Maxwell’s equations)的磁矢势场(magnetic vector potential field)的运动推导出一种可能的解决办法,即:因子 ![]() 是一个可选的迹象[3]。(注:磁矢势又称向量磁位,是电磁学上的一个三维空间向量的物理量。磁矢势的旋度是磁场。使用磁矢势可取代磁场在麦克斯韦方程组的角色)
是一个可选的迹象[3]。(注:磁矢势又称向量磁位,是电磁学上的一个三维空间向量的物理量。磁矢势的旋度是磁场。使用磁矢势可取代磁场在麦克斯韦方程组的角色)
在1899-1904年期间,由于迈克尔逊- 莫雷实验(Michelson-Morley experiment)的零结果,洛伦兹不得不用“v/c”的概念来解释他的理论,洛仑兹提出了一个假设,认为一切在“以太”中运动的物体都要沿运动方向收缩。由此他证明了,即使地球相对“以太”有运动,迈克尔逊也不可能发现它。这最终形成了数学方法的洛伦兹变换。1904年,洛仑兹提出:通过“以太”的运动物体,纵向线度发生收缩(平行运动方向),其收缩的比例恰好使“以太”流的影响被抵消。这一假说称为收缩假说[4],由洛伦兹和斐兹杰惹所提出。根据他的设想,观察者相对于“以太”以一定速度运动时,长度在运动方向上发生收缩,抵消了不同方向上由于“以太”所造成的光速差异,这样洛仑兹就在不抛弃“以太”概念的前提下解释了迈克尔逊-莫雷实验的结果。其理论公式如下:
![]() (l0 是在静止“以太”中的长度)
(l0 是在静止“以太”中的长度)
在1905年,昂利•庞加莱(Henri Poincare)发表了他的第一篇关于相对论的论文。该论文的课题是「部分运动学的,部分动力学的」,并包括洛伦兹关于洛伦兹变换(实际上是庞加莱给它这个名字的)的证明的更正。庞加莱实际比爱因斯坦的工作更早一步,并起草了一个狭义相对论的简略版。在1898年,在「时间的测量」中,他阐述了相对论原理,根据这个原理,没有机械或电磁试验可以区分匀速运动的状态和静止的状态[5]。和荷兰理论家洛伦兹的合作中,他把时间的物理推向极限来解释快速运动的电子的行为。在1909年,洛伦兹也对此作了相似的理论阐述[6]。
三 洛伦兹因子的最终形式
1900年,庞加莱指出:迈克尔逊- 莫雷实验结果表明在“以太”中的绝对运动和相对运动的形式是无法区别的,并首先提出了“相对运动原则”和“相对空间”的观点。对此,在1904年,洛伦兹发表了一篇重要文章来解释他的理论,指出电磁场的作用是独立于整个运动体系的[7]。
1905年,庞加莱指出电磁场的洛伦兹方程不能满足洛伦兹协变性或洛伦兹共变性(Lorentz covariance)。他纠正了洛伦兹关于电荷密度和电流密度的变换公式,通过使用变换群属性(数学上的“群公理”)和设定光速的一致性,证明了麦克斯韦-洛伦兹方程组(Maxwell-Lorentz equations)的洛伦兹协变性。由此,庞加莱推导出了洛伦兹因子的最终形式[8]:![]()
![]()
尽管庞加莱也涉及了最初的“四维”概念,但最终他没有去继续这方面的理论,相反,这方面的工作是由是由赫尔曼•闵可夫斯基(Hermann Minkowski)完成的。
四 转变为相对性的过程
1905年,爱因斯坦发表了现在称之为“狭义相对论”的论文,通过分析检验空间和时间坐标在物理理论中应用的基本意义,爱因斯坦发现了洛伦兹变换中的“效应的”坐标其实就是相对运动参考系(而言)的惯性坐标。因此,爱因斯坦认为:不能观察到的“以太”(假设“以太”存在)是不需要的。在相对性原理和光速不变原理的基础上,爱因斯坦推导出和洛伦兹变换有着同样数学形式的变换式[11]。
1907年,闵可夫斯基以四维时空的观点说明了相对性的关系是很自然的解释,四维时空间隔就是毕达哥拉斯定理(勾股定理)的延伸。在相对论里,四维矢量 (four-vector) 是一种实值四维矢量空间里的矢量。这四维矢量空间称为闵可夫斯基时空。四维矢量的分量分别为时间与三维空间的位置。在闵可夫斯基时空内的任何一点,都代表一个事件,可以用四维矢量表示。应用洛伦兹变换,可以使对于某惯性参考系的四维矢量,经过平移,旋转,或递升(Lorentz boost),变换到对于另一个惯性参考系的四维矢量。所有这些平移,旋转,或递升的集合形成了庞加莱群(Poincaré group)。所有的旋转,或递升的集合则形成了洛伦兹群(Lorentz group)[12]。
由于普遍认为爱因斯坦和闵可夫斯基对“变换”的阐述更具整体性和自然性,导致狭义相对论被迅速而广泛地接受,并失去了对“以太”理论的兴趣。
【结果及讨论】
通过对洛仑兹因子的考证,可以得出以下二个结果:
一 洛仑兹因子的假设前提在洛仑兹的洛仑兹变换和狭义相对论的(变换)方程中是不同的
洛仑兹为了解释“以太漂移实验”和“迈克尔逊- 莫雷实验”,假设与“以太”静止者和与“以太”运动者之间会有时间或长度的不同,它们之间没有相对性,与“以太”静止者的时间或长度为“真”,运动者的时间或长度只是辅助变量,只用于运动系的计算过程。他认为“以太”是需要的,只是可能“测不出”。洛仑兹变换的假设前提实际上只用到运动速度相对性和光在惯性运动速度相等这两个假设上。其“r”因子是假设出来的。
爱因斯坦和闵可夫斯基的狭义相对论理论对洛仑兹因子并没有进行假设,而是先提出四维时空的结构模式,按相对性原理和光速不变的原理的假设,基于光速是有限的,那么,则相对运动的系之间必然有对时间或长度的相对性结论。也可以说,如果狭义相对论的其它前提(或假设)是正确的话,则“t’=rt”是必然的,其“r”因子是推理出来的。
二 洛仑兹的洛仑兹变换和狭义相对论的变换方程中的数学推导前提也是不同的
洛仑兹的洛仑兹变换基本上庞加莱进行的数学推导,在假设洛仑兹因子的前提下,庞加莱仅设定了“光速一致”的条件就推导出了他首先命名的洛仑兹变换,实际上今天许多书或资料中提及的洛仑兹变换推导过程就是这样的形式。这里有二点值得注意:一是这种变换并没有否定“以太”或没有强调“以太”是否必要,按庞加莱的最初意图来看,他是认为“以太”存在的基础上进行推导的;二是在数学变换的推导上假设了“静系”与“运动系”,也可以说没有强调运动是相对性的。无疑,这是与狭义相对论的理论有本质的不同的。尽管爱因斯坦最初期也推导出有同样数学形式的变换,但爱因斯坦强调了不需要“以太”和强调了相对性原理。如果在四维时空的基础上进行推导,则狭义相对论的变换方程完全不同于洛仑兹的洛仑兹变换了,它们在物理理论上的前提是完全不同的。
【结论及建议】
一 对洛伦兹因子的物理意义,存在二种截然不同的观点:
(一)“以太”观的洛伦兹变换
从上述的考证过程中可以了解到:最初的意义上的洛伦兹因子是基于以洛伦兹为代表的“以太”理论推导的。洛伦兹和庞加莱他们一生都没有放弃“以太”理论。
庞加莱在1900年就指出:“以太”是协调洛伦兹变换和牛顿第三定律所必须的;在1912年他发表的“量子理论”一文中,他曾十次提到“以太”,并认为光就是“以太”发光的振荡(luminous vibrations of the ether)[9]。
洛伦兹一直认为有特别的参照系存在,在这个特别的参照系(与“以太”静止)中的时钟才是真正的时间(“real time”),如果相对性(系统)原理是可以接受的话,实验上是无法区分这样的系统的[10]。他去世前不无解嘲地说:这个时刻(去世)对他来讲将是唯一的。
(二)“时空”观的洛伦兹变换
爱因斯坦在抛弃以太、以光速不变原理和狭义相对性原理为基本假设的基础上建立了狭义相对论。狭义相对论认为空间和时间并不相互独立,而是一个统一的四维时空整体。在狭义相对论中,整个时空仍然是平直的、各向同性的和各点同性的。结合狭义相对性原理和上述时空的性质,也可以推导出有同样数学形式的洛仑兹变换。
二 物理学上应该正式区分这二种学术观点
物理学上应该把“以太”观的洛伦兹变换和“时空”观的洛伦兹变换作出区别,尽管它们有着同样的数学形式,但它们的物理(意义)内涵却完全不同。如果“以太”观的变换仍然称之为“洛伦兹变换”,则“时空”观的变换就应该称之为“爱因斯坦变换”或称之为“时空变换”或“狭义相对论变换”,以严格区分它们所代表的物理意义之不同。区分这二种学术观点至少有以下好处:
(一)减少学术观点讨论时的概念混淆
如果我们今天还把狭义相对论的“变换”称之为“洛伦兹变换”,无疑就掩盖了以洛伦兹为代表的学术观点,尽管“以太”“不能观察到”,那么,谁又能通过实验证明“四维时空”或观察到“四维时空”呢?同样不能。至今,没有谁证明了以洛伦兹为代表的学术观点是完全错误的,所以,不能因为狭义相对论而掩盖了以洛伦兹为代表的学术观点。以洛伦兹为代表的学术观点同样可以解释“尺缩”和“时慢”,狭义相对论并不是唯一的理论解释。
(二)洛伦兹“如果相对性(系统)原理是可以接受的话,实验上是无法区分这样的系统的[10]”仍然是对狭义相对论的挑战。这种实验如何与狭义相对论理论统一起来至今希望渺茫。在二个系中可以用相对性原理解释,但实际上常常可以引入二个以上的系来作参照,那么,这种情形下,相对性原理显然面临挑战。相反,区分和保留“以太”观的洛伦兹变换可以有利于这种解释或解释得更好些。
(三)由于洛伦兹的洛伦兹因子和“以太”理论也可以解释了迈克尔逊- 莫雷实验结果,不能因此而认为该实验是对“以太”理论的否定。如果庞加莱“光就是‘以太’发光的振荡(luminous vibrations of the ether)[9]”成立或被赋予新的内涵或解释意义,“以太”论将重新获得理论上的重视。
当今,洛伦兹变换已经成为狭义相对论的代名,“尺缩”和“时慢”完全来自洛伦兹变换的推导,因为它和狭义相对论有同样的数学形式,实验上是无法区分洛伦兹变换和狭义相对论在理论上的区别的。然而,它们之间是有区别的,并且有着本质的区别,那就是洛伦兹变换是基于“以太”尚没有办法测出的假设(或基础)上,只是这种“测不出”正好与狭义相对论吻合,以至狭义相对论时常掩盖了洛伦兹变换的原始思想观点,当然,相对论的时空观和广义相对论的形成也是重要原因。
知其源,还要知其所以然。是正本清源的时候了,应该重新命名“爱因斯坦变换”或“狭义相对论变换”或“时空变换”以区别洛伦兹的洛伦兹变换,它们在物理理论的内涵上有本质的不同。
*以太(或译乙太;英语:ether或aether)是古希腊哲学家所设想的一种物质,是一种被假设的电磁波的传播媒质。
【参考文献】
1.Born, Max (1964), Einstein’s Theory of Relativity, Dover Publications, ISBN 0486607690
2.http://en.wikipedia.org/wiki/Lorentz_ether_theory
3.Darrigol, Olivier (2005), “The Genesis of the theory of relativity”, Séminaire Poincaré 1: 1–22
4.Darrigol, Olivier (2000), Electrodynamics from Ampére to Einstein, Oxford: Clarendon Press, ISBN 0198505949
5.Poincaré, Henri (1898/1913), “The Measure of Time”, The foundations of science, New York: Science Press, pp. 222–234
6.Lorentz, Hendrik Antoon (1909/16), The theory of electrons and its applications to the phenomena of light and radiant heat at the Internet Archive, Leipzig & Berlin: B.G. Teubner
7.Lorentz, Hendrik Antoon (1892/1907), “Die relative Bewegung der Erde und des Äthers”, Abhandlungen über Theoretische Physik, Leipzig: B.G. Teubner, pp. 443–447
8.http://en.wikipedia.org/wiki/Henri_Poincar%C3%A9
9.Poincaré, Henri (1901a), “Sur les principes de la mécanique”, Bibliothèque du Congrès international de philosophie: 457–494. Reprinted in “Science and Hypothesis”, Ch. 6-7.
10.Poincaré, Henri (1902), Science and hypothesis at the Internet Archive, London and Newcastle-on-Cyne (1905): The Walter Scott publishing Co.
11.《Relativity 相对论》 [美] 约翰•施塔赫尔主编
12.四维矢量 (four-vector) 维基百科 http://zh.wikipedia.org/zh-cn/
1st published >>华夏科技电子期刊《反相吧刊》 (add321.com)<<

