ORIGINAL LORENTZ FACTOR
Definition
The Lorentz factor or Lorentz term is a quantity expressing how much the measurements of time, length, and other physical properties change for an object while that object is moving. The expression appears in several equations in special relativity, and it arises in derivations of the Lorentz transformations. The name originates from its earlier appearance in Lorentzian electrodynamics – named after the Dutch physicist Hendrik Lorentz.
It is generally denoted γ (the Greek lowercase letter gamma). Sometimes (especially in discussion of superluminal motion) the factor is written as Γ (Greek uppercase-gamma) rather than γ.
The Lorentz factor γ is defined as

where:
- v is the relative velocity between inertial reference frames,
- c is the speed of light in a vacuum,
- β is the ratio of v to c,
- t is coordinate time,
- τ is the proper time for an observer (measuring time intervals in the observer’s own frame).
This is the most frequently used form in practice, though not the only one (see below for alternative forms).
To complement the definition, some authors define the reciprocal
Occurrence
Following is a list of formulae from Special relativity which use γ as a shorthand:
- The Lorentz transformation: The simplest case is a boost in the x-direction (more general forms including arbitrary directions and rotations not listed here), which describes how spacetime coordinates change from one inertial frame using coordinates (x, y, z, t) to another (x′, y′, z′, t′) with relative velocity v:
Corollaries of the above transformations are the results:
- Time dilation: The time (∆t′) between two ticks as measured in the frame in which the clock is moving, is longer than the time (∆t) between these ticks as measured in the rest frame of the clock:
- Length contraction: The length (∆x′) of an object as measured in the frame in which it is moving, is shorter than its length (∆x) in its own rest frame:
Applying conservation of momentum and energy leads to these results:
- Relativistic mass: The mass m of an object in motion is dependent on
and the rest mass m0:
- Relativistic momentum: The relativistic momentum relation takes the same form as for classical momentum, but using the above relativistic mass:
- Relativistic kinetic energy: The relativistic kinetic energy relation takes the slightly modified form:
As 


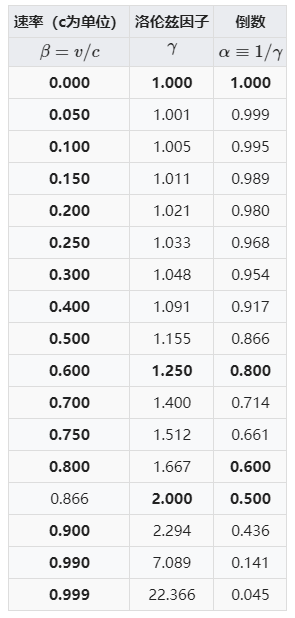
洛伦兹因子是一个出现在狭义相对论中的速记因子,得名于荷兰物理学家亨德里克·洛伦兹,被用于计算时间膨胀、长度收缩、相对论质量等相对论效应。
洛伦兹因子定义为:
其中
一些作者另外定义了洛伦兹因子的倒数:
可用于速度相加推导。
相对论性条件(近光速)下,物体的总能量


其中
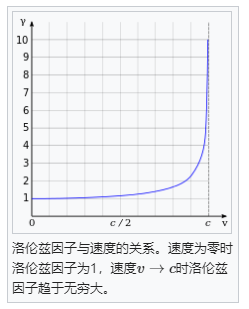














 定义相似。
定义相似。